Finding the Sum of a Power Series

source: http://www.math.toronto.edu/mathnet/questionCorner/powerseries.html

The series you have described is not a geometric series. It is an example of a more general class of series called power series, which are of the form 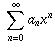where the coefficients 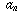don't depend on the variable x. In your example, 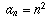. A key fact about power series is that, if the series converges on an interval of the form |x| < R, then it "converges uniformly" on any closed subinterval of that interval. I won't attempt to explain what that means, but will mention instead an important consequence (which is not always true for series that are not power series): the series can be integrated and differentiated term by term, in the sense that, if you define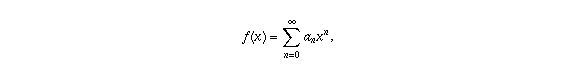

then

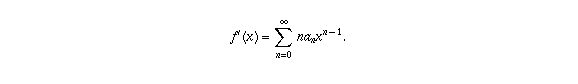
This means that, if you start with the geometric series 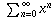which is known to converge to 1/(1-x) when |x| < 1 (as described in the answer to another question), the following is true for all |x| < 1 by differentiating both sides of the equation: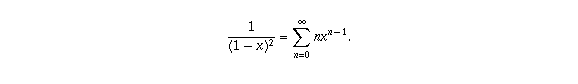

If you multiply both sides by x you get something close to what you want:

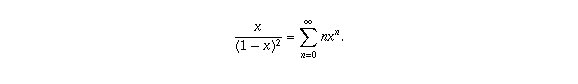
Differentiating both sides again and multiplying by x again gives you what you want:

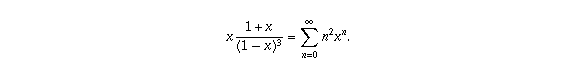
Therefore, your series converges to 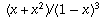, provided |x| < 1. (If |x| > 1, it diverges).
This particular technique will, of course, work only for this specific example, but the general method for finding a closed-form formula for a power series is to look for a way to obtain it (by differentiation, integration, etc.) from another power series whose sum is already known (such as the geometric series, or a series you can recognize as the Taylor series of a known function).
Most series don't have a closed-form formula, but for those that do, the above general strategy usually helps one to find it.